在金融衍生品市場中，選擇權的價格波動性高，且對於標的資產價格的變動十分敏感。選擇權希臘字母指標正是為了量化這些變動對選擇權價格的影響而設計。每一個希臘字母代表的是選擇權價格對於某一特定標的資產屬性變化的敏感度，例如股票價格和波動性。

這些屬性是交易者需要控制的風險組成部分，以管理其投資組合的整體風險。希臘字母指標提供了一種簡便的計算方法，成為衍生品交易者廣泛使用的工具，尤其在組合避險方面極為實用。這使投資者能夠保護他們的投資免受市場不利變動的影響。

🚀【選擇權交易】掌握希臘字母指標，交易效率倍增秘訣📈

---

在選擇權市場中想要站穩腳步，了解希臘字母指標是你的必修課！這些指標能幫助你預測選擇權價格的變動，讓你的投資策略更上一層樓。來看看怎麼利用它們吧！👇

1. Delta Δ – 方向感的指南針🧭
   Delta值告訴你，當標的資產價格變動時，選擇權價格會如何改變。高Delta值的選擇權，隨著股價小幅波動，價格變化更顯著。
2. Gamma Γ – Delta的加速度計⚡
   Gamma影響Delta的變化速度。高Gamma值意味著Delta值隨股價變化更快，使得選擇權價格對股價變化更敏感。
3. Theta Θ – 時間的沙漏⏳
   每過一天，Theta告訴你選擇權價值會減少多少。對於賣方來說，時間流逝是你的盟友；對買方則是挑戰。
4. Vega 𝜈 – 波動率的風向標🌬️
   Vega衡量選擇權價格對波動率變化的敏感度。在市場波動期間，了解Vega可以幫助你做出更明智的交易決策。
5. Rho ρ – 利率變動的晴雨表🌦
   Rho顯示利率變化如何影響選擇權價格。在預測利率變動時，這個指標可以幫助你調整交易策略，尤其對長期選擇權影響更大。

---

掌握這些希臘字母指標，讓你的選擇權交易策略更加科學化、系統化。無論是資深投資者還是市場新手，這些基礎知識都是你成功的關鍵。開始你的選擇權交易之旅，讓這些指標成為你的利器吧！📚💼

Delta – 方向感的指南針🧭

• 價格變動敏感度：Delta 代表標的資產價格每變動一單位時，選擇權價格的預期變動量。
• 範圍：對於買權，Delta 的範圍在 0 到 1（或 0% 至 100%）之間；對於賣權，Delta 範圍在 -1 到 0（或 -100% 至 0%）之間。
• 實值與虛值：實值選擇權的Delta較接近於 1（買權）或 -1（賣權），而虛值選擇權的Delta則接近於 0。
• 到期時間影響：隨著選擇權接近到期，實值選擇權的Delta會趨近於 1 或 -1，反映出其價格變得更加敏感於標的資產價格的變動。
• 波動性影響：高波動性環境下，選擇權價格對標的資產價格的變動較為敏感，因此Delta值可能會有較大的變化。
• 避險策略：Delta是避險（Hedging）策略中的一個關鍵參數，用於計算達到Delta中性（Delta Neutral）策略所需的標的資產數量。
• 動態調整：因為標的資產價格的變動，Delta值是動態變化的，需要定期調整避險頭寸以維持避險策略的有效性。
• 預期方向：Delta值可以被解讀為選擇權結算時結束於實值的預期概率。

Delta 指標用來衡量標的資產價格每變動 1 元時，選擇權價格改變的幅度。對於一個 Delta 值為 0.50 的選擇權，當標的資產價格上升或下降 1 美元時，該選擇權的價格預期將變動大約 0.50 美元。買入買權(Buy Call)的 Delta 值介於 0 至 1.00 之間，而買入賣權(Buy Put)的 Delta 值則介於 0 至 -1.00 之間。對於賣出選擇權的情況，由於投資者實際上持有負數量的合約，因此賣出賣權具有正 Delta；賣出買權則有負 Delta（技術上是正 Delta 乘以負合約數量）。

讓我們透過一個例子來說明買權 Delta 的變化：

某天，XYZ 公司的$60 Call的Delta值為0.55。該$60 Call的當前價格為3.50元。若 XYZ 股票價格上漲$1元，該買權價格將上漲$0.5，計算方式為：1.00 美元 x 0.55 = 0.55 美元。因此，預期的買權價值將從目前的 3.50 美元增加到 4.05 美元。

若 XYZ 股票價格上漲$0.60，該買權價格將上漲$0.6×0.55=$0.33。因此，預期的買權價值將從目前的$3.50 增加到$3.83 美元。

Delta vs 標的價格

然而隨著價格的變動，Delta 本身也會變化。舉例來說，一個 Delta 為 0.5 的選擇權，當標的資產價格上漲1元，選擇權的價格上漲 0.5，同時 Delta 也可能上漲至 0.6。所以，越「價外」(簡稱OTM; 註一)的Call選擇權的Delta越低，越價內(簡稱ITM)的Call選擇權的Delta越高。

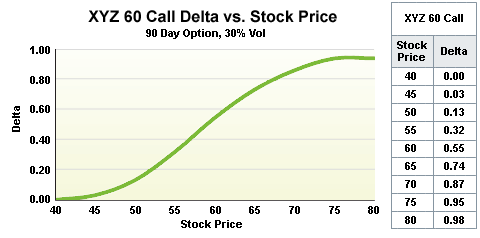
用Delta估算未來價格概率

Delta 不僅反映了選擇權價格對標的資產價格變動的敏感度，還可用來估算股票在到期時處於「價內」的概率。因此，Delta 常被視為未來價格概率的一種替代指標。

例如，一個 Delta 值為 0.3 的買權，大致可以解讀為該選擇權的行權價格(Strike Price)在到期時有 30% 的概率會處於價內，相對地，有 70% 的概率會處於價外。一個 Delta 值小於 0.10的選擇權，被認為很難在任何時點處於價內，需要標的價格有強烈的價格變動才能在到期時有價值。

在賣出選擇權時，Delta 可以快速提供選擇權成功的概率近似值。一個 0.30 的 Delta 表示大約有 30% 的概率到期時處於價內（或有 70% 的概率到期時處於價外）。

因此，賣出一個 0.30 Delta 的買權，大致意味著有 70% 的成功概率和 30% 的失敗概率。

註一：價外(Out-of-The-Money, 簡稱OTM)意思是買權(Call)選擇權的行權價格高於目前標的資產價格，或是賣權(Put)選擇權的行權價格低於目前標的資產價格。價內(In-The-Money, 簡稱ITM)意思是買權(Call)選擇權的行權價格低於目前標的資產價格，或是賣權(Put)選擇權的行權價格高於目前標的資產價格。

Delta vs 隱含波動率

隨著隱含波動率的提升，Delta 傾向於向 0.50 靠攏，因為市場認為更多的行權價有可能在到期時變成價內，這是基於對標的資產潛在移動的預期。

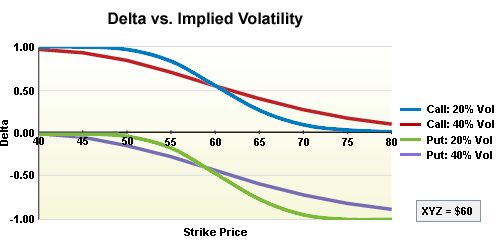
例如，當 XYZ 股票價格為 21 美元且隱含波動率為 30% 時，20 買權的 Delta 可能是 0.60。如果隱含波動率上升到 40%，由於交易者預期行權價在到期時變成價外的可能性增加，Delta 可能會下降到 0.55。

當隱含波動率較高時，更多的執行價位會進入「波動」範圍內，使得更多 Delta 接近於 0.50。相對地，隱含波動率較低的股票，價內選擇權的 Delta 值會較高，價外選擇權的 Delta 值則較低。

Delta vs 時間

到期日剩餘時間同樣會影響 Delta 值。對於同一執行價的買權，到期時間較長的價內買權總會有一個較低的 Delta 值，相比之下，到期時間較短的同一執行價買權的 Delta 值會較高。對於價外買權則恰好相反；到期時間較長的買權會有較高的 Delta 值，相比於到期時間較短的選擇權。

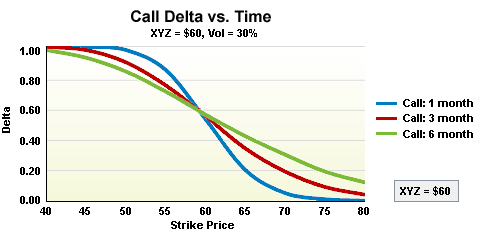
隨著到期日逼近，假設其他因素保持不變，價內買權的 Delta 值會逐漸增加至 1.00，平價買權的 Delta 值大致維持在 0.50 左右，而價外買權的 Delta 值則會趨近於 0。

Gamma – Delta的加速度計⚡

• Delta的變動率：Gamma 表示當標的資產價格變動一單位時，選擇權的Delta值將如何變化。
• 最高值在價平選擇權：Gamma 對於接近價平（標的資產價格接近選擇權行使價）的選擇權最為敏感，這時Gamma值通常最高。
• 實值與虛值選擇權的Gamma值：實值和虛值選擇權的Gamma值較低，因為它們的Delta值變動較不敏感。
• 選擇權到期時間的影響：隨著選擇權接近到期，Gamma值會增加，特別是對於價平選擇權，反映了Delta變動的加速。
• 避險重要性：Gamma 揭示了避險策略需要多頻繁地調整以維持Delta中性。高Gamma值意味著需更頻繁地調整避險頭寸。
• 選擇權組合管理：對於選擇權組合管理者來說，瞭解Gamma幫助於預測市場波動對選擇權組合Delta值的影響。
• 風險指標：Gamma可以被視為風險指標，高Gamma值選擇權的Delta值變化較快，意味著更高的價格波動性和風險。
• 策略設計：在設計選擇權策略時，瞭解Gamma幫助交易者預測價格變動對策略表現的影響，並作出相應調整。

Gamma描述的是當標的資產價格每變動$1時，Delta 的預期變化量。投資者可以透過Delta了解標的資產價格變動$1對選擇權價格的影響，但要瞭解同樣$1變動下 Delta 如何改變，就需要參考Gamma。Gamma 的範圍在0到1之間。由於Delta的最大值為1，Gamma也不會超過1，因為Gamma代表的是Delta預期的變化量。

• 買入買權和買入賣權都會產生正Gamma
• 賣出買權和賣出賣權則會有負Gamma

以一個假設的例子來說，XYZ股票目前價格為$50。XYZ 1 月 $50 Call 的交易價格為 2 美元，Delta 為 0.50，Gamma 為 0.06。如果 XYZ 的價格上漲到$51，投資者可以估計這個 $50 Call 的買權現在大概值 2.50 美元。在 XYZ 價格為 51 美元時，這個 $50 Call 的新 Delta 應該是大約 0.56（Delta 0.5 + Gamma 0.06 )。

Gamma vs 資產價格

• Gamma 的最大值出現在價平(ATM)。
• 不論價內或價外，離價平越遠，Gamma越低

深價內或遠價外的選擇權，其 Gamma 比價平選擇權來得低。深價內選擇權已經擁有高正或高負的 Delta。如果這些選擇權變得更深價內，Delta 會向 1.00（或對於賣權則為 -1.00）移動，而 Gamma 會因為 Delta 無法超過 1.00 而減少。如果股票價格向深價內選擇權的行權價移動，Gamma 會增加，而 Delta 大約會按目前 Gamma 的量減少。

Gamma vs 時間

• 近月價平選擇權Gamma較高
• 遠月價平選擇權的Gamma較低

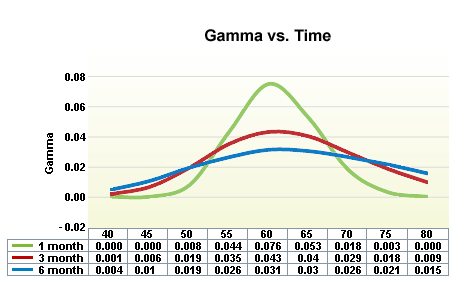
在更長期的選擇權，如LEAPS中，Gamma 較低，因為剩餘時間較多，更多的行權價有可能在到期時變成價內。價平選擇權的 Delta 通常對標的資產價格變動最敏感（因此 Gamma 較高）。當股票價格恰好在到期時達到某個執行價時，該選擇權的 Gamma 將達到最高，因為 Delta 有可能從 1.00 快速變化到 0 或反之，隨著標的資產穿過執行價。在這些情況下，隨著標的資產價格在執行價位附近波動且到期日接近，Gamma 可能極高，因為 Delta 的變化非常迅速。

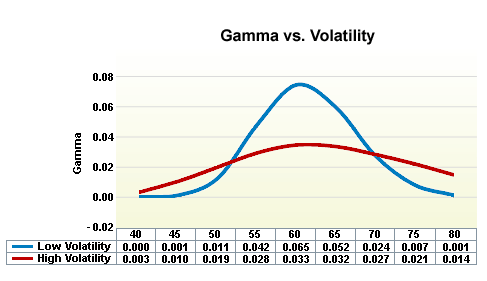
Gamma vs 隱含波動率

• 隱含波動率越低，價平選擇權的Gamma越高

隱含波動率的變化也會影響 Gamma。隨著隱含波動率的降低，價平買權和賣權的 Gamma 增加。當隱含波動率提高時，價內和價外的買權和賣權的 Gamma 將會減少。這是因為低隱含波動率的選擇權在標的資產移動時，Delta 的變化會更加戲劇性。高隱含波動率的標的產品，在價格變動時 Delta 的變化較小，因為預見到更多的價格移動可能性。

Gamma 擠壓 (Gamma Squeeze)

Gamma 擠壓發生在選擇權合約突然間需求大增時，導致該選擇權的 Gamma 值增加。而股票價格上漲時，賣出選擇權的造市商，需要買入股票來對沖管理他們持有的賣出選擇權。此舉進一步加大股價的上漲，最後造成價格井噴。

以 GME 事件為例，短期擠壓推高了價格。大量零售交易者同時買入 GME 的買權。賣出這些買權的造市商被迫買入股票來對沖 GME 價格的上漲。更多的買權購買導致交易商在標的股票中進行更多的買入。這一循環導致 GME 價格的大幅移動。

Vega – 波動率的風向標🌬️

• 波動率的影響：Vega 表示當標的資產的隱含波動率上升1個百分點時，選擇權價格的變動量。
• 最高值於平價選擇權：Vega 對於平價選擇權（標的資產價格接近選擇權行使價）最敏感，這些選擇權的Vega值通常最高。
• 到期時間的影響：Vega 隨著選擇權到期時間的延長而增加，長期選擇權比短期選擇權對波動率的變化更為敏感。
• 波動率水平的影響：在高波動環境下，選擇權的Vega值可能會因為價格已經包含了較大的波動性預期而相對較低。
• 策略設計與風險管理：理解Vega對於設計避險策略和管理選擇權組合的波動率風險至關重要。
• 市場預測工具：Vega 可用於預測市場對未來波動性的預期，幫助交易者把握交易機會。
• 標的資產性質的影響：不同標的資產的選擇權Vega值會有所不同，反映了不同市場和資產對波動率變化的敏感度差異。
• 隱含波動率變化的風險：Vega 揭示了選擇權價格對隱含波動率變化的敏感度，是風險管理中不可忽視的因素。

Vega 用來衡量選擇權價格對隱含波動率變化的敏感度。隱含波動率以百分比表示，是定價模型中的關鍵變量。隱含波動率與過去的實際歷史或統計波動率沒有直接關聯，它更多的是對未來走勢的預測。在不確定性增加或預期有重大新聞公布時，隱含波動率會上升；而在市場平靜時期，則傾向於下降。一些投資者會使用股票的歷史波動率來預測隱含波動率應該處於的水平，但市場最終決定了當前的隱含波動率水平。此外，即使標的資產沒有變動，Vega 和隱含波動率也可能變化。

• 近月Vega較低，遠月Vega較高

Vega 衡量的是基於 1%（100 基點）隱含波動率假設變化所導致的價格增減量。遠期選擇權比近期選擇權有更高的Vega。長期選擇權通常更昂貴，1% 的隱含波動率變化對於價格的影響金額比低價的選擇權來得大。例如，假設 XYZ 股價為$50，近月 $50 Call交易價格為$2，而12個月後的$50 Call交易價格為$5，更昂貴的買權對 1% 隱含波動率的變化影響更為顯著。若要使價格上漲相同的金額，近期選擇權的隱含波動率需要上升約 2.5 倍於長期選擇權。

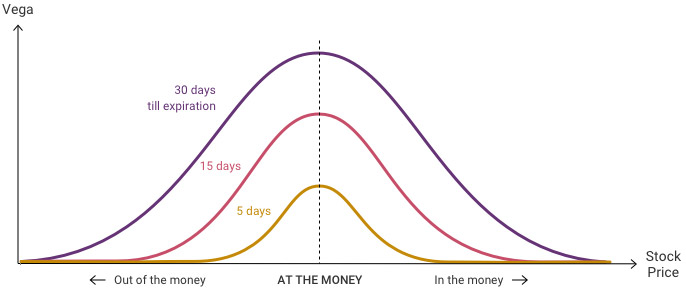
舉例來說，假設 XYZ股票價格$50，一個到期日為12月的Call隱含波動率為 30%，Vega 為0.15，選擇權價格為$4。如果隱含波動率瞬間上升 2% 至 32%，則選擇權價格上漲至$4.3 ( $4 + Vega 0.15 x 2)。

• Vega的高峰在價平
• 隨著選擇權接近到期，Vega 值會下降

bid-ask-spread vs Vega

如果一個選擇權的 Vega 值大於買賣差價，那麼這個選擇權被認為提供了有競爭力的差價。反之亦然。Vega 還讓我們知道基於標的資產的波動性變化，選擇權價格可能的波動幅度。

假設ABC股票在一月份每股交易價格為$50，而二月份$52.50 Call的委買價(bid)為$1.50，委賣價(ask)為 $1.55。假設該選擇權的 Vega 值為 0.25，隱含波動率為 30%。因為買權差價小於 Vega，代表市場價差合理。過高的差價可能使得進出交易更加困難或成本更高。

如果隱含波動率上升1%，則該選擇權的委買價和委賣價應分別上升到$1.75($1.5+Vega 0.25)和$1.80。如果隱含波動率下降 5%，則委買價和委賣價理論上應分別下降至$0.25($1.5 – (Vega 0.25 x 5)和$0.30。波動性增加使得選擇權價格上升，而波動性下降則使選擇權價格下跌。

Theta – 時間的沙漏⏳

• 代表時間價值衰減：Theta 表示理論上選擇權溢價，在條件不變情況下，每天可能衰減的金額。
• 非線性衰減：Theta 的衰減速率隨著到期日的接近而加快，尤其是到期日最後階段特別顯著。
• 到期日效應：接近到期時，選擇權的時間價值迅速衰減，最終在到期日時選擇權只剩下內在價值（如果有的話）。
• 隱含波動性影響：隱含波動性的變化會影響Theta值，高隱含波動性環境下Theta值較高。
• 價平選擇權敏感性：價平選擇權對時間價值衰減最為敏感，而深度價內或深度價外選擇權的時間價值衰減則相對較小。

Theta用以表示在其他因素不變的前提下，選擇權溢價每日可能下降的金額，這個衰減量以實際美金或溢價量來衡量。舉例來說，一個Theta值 -0.01 的選擇權，代表該選擇權溢價在所有條件不變的情況下，將在一天後下跌 $0.01。

Theta所呈現的時間價值衰減並非線性過程。隨著到期日的臨近，理論上的衰減速率會逐漸加快。因此，Theta顯示的衰減量起初會比較緩慢，但在接近到期時會明顯加速。到期時，選擇權將不再具有時間價值，只按內在價值進行交易（如果有的話）。值得一提的是，定價模型會考慮週末效應，導致選擇權在五個交易日內實際上會經歷七天的時間價值衰減。然而，業界並無一致的時間衰減方法，不同的模型對時間衰減的展現各不相同。

以XYZ公司股價$50、行權價$50的買權交易價為$3、Theta值為-0.05為例，投資者預期在其他條件不變的情況下，該選擇權每天會損失大約$0.05的時間價值。隨著到期日的接近。下圖是Theta隨到期日變化而放的的圖表：假設在XYZ股價為$50、行權價$50的買權、使用40%的恆定隱含波動率。隱含波動率和標的價格保持不變，Theta所代表的時間價值衰減會以指數型成長。

Theta vs 時間

時間溢價在到期前30天左右開始迅速衰減，剩餘到期時間最少的選擇權衰減最快。處於價平狀態的買權對於標的資產價格的停滯最為衰減嚴重。

Theta vs 隱含波動率

產品的隱含波動性將決定其時間溢價的多少，進而影響Theta值。一般來說，隱含波動率越高，Theta值也越高。選擇權的高隱含波動率，是因為實際的歷史波動性，或者是因為即將發布的盈利報告、產品公告等原因。下面是一張圖表，展示了不同隱含波動率下的大致Theta值：

投資者應當理解，高隱含波動率往往伴隨著更大的市場不確定性，而這種不確定性是Theta值增加的主要驅動力。在評估選擇權策略時，考慮隱含波動率對Theta的影響是至關重要的，特別是在面對重大市場事件或數據公布時。

Theta vs 行權價位置

價平選擇權（At-the-money options）對時間價值的衰減最為敏感。正如以上圖表所示，深度價內（deep-in-the-money）或深度價外（far out-of-the-money）的選擇權由於時間溢價較少，因此其時間價值的衰減也會非常有限。此外，由於買權（call options）具有無限上升空間，買權的價格往往會略高於賣權溢價。

選擇權的時間價值衰減是選擇權交易中的一個關鍵考量，特別是對於位於價平的選擇權。投資者在考量選擇權交易策略時，應該密切關注隱含波動性和時間價值衰減的影響，這對於有效管理風險和捕捉市場機會至關重要。

Theta策略

Theta 是許多選擇權交易策略的基礎。透過不同的買賣組合，可以影響時間價值衰減的速度。

單一買入看漲選擇權或買入看跌選擇權時，Theta代表該選擇權價格每日的減少量，數字為負值。反之，賣出選擇權時，時間價值衰減對賣方則是視為獲利，Theta為正值。買入單一部位的投資組合面臨大量的時間價值衰減。在市場波動緩慢的日子裡，由於Theta（時間價值衰減）和Vega（波動率的變化）同時下降，投資組合的價值可能會顯著減少。

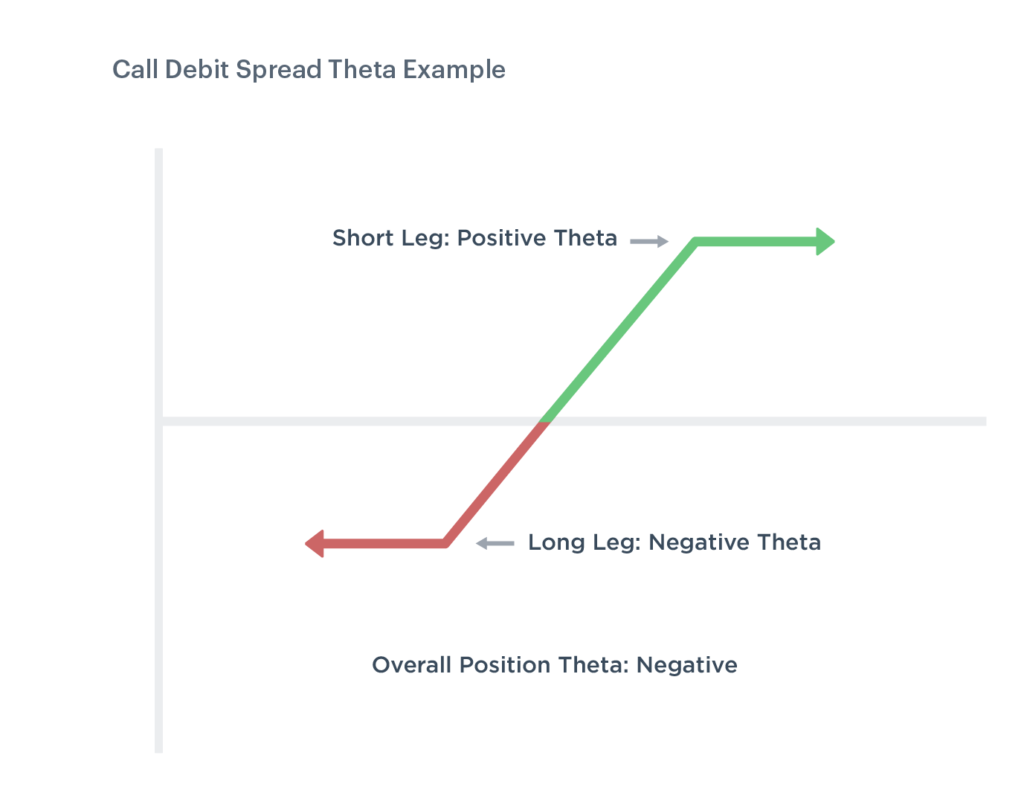
多頭差價策略則是組合兩個選擇權，例如同時買入一個價平買權(Theta -0.16)與賣出一個價外10美元的賣權(Theta -0.1)，這樣的策略Theta值為-0.06。這是因為賣出合約的Theta值對賣方有利，在計算Theta總和時，變成正數，所以Theta總和是-0.16+0.1=-0.06。儘管多頭差價策略仍然會由時間價值衰減，但由於賣出選擇權的存在，時間價值衰減的速度減少了。

Rho – 利率變動的晴雨表🌦

• Rho 衡量選擇權價格對利率變動的敏感度。
• 對於買入買權，Rho 為正，意味著利率上升時，買權的溢價會增加。
• 對於買入賣權，Rho 為負，意味著利率上升時，賣權的溢價會下降。
• 選擇權交易者通常忽略Rho，因為在大多數選擇權策略的執行期間，利率不太可能有大的變動。
• 當考慮購買或出售長期選擇權（如LEAPS）時，若預期利率將變動，需要考慮Rho。

Rho 用於衡量選擇權價格對零風險利率變動的敏感度，三個月期的美國國庫券通常被作為無風險利率的標準選擇。Rho 通常被期權交易者忽略，因為在大多數選擇權策略的執行過程中，利率不太可能發生重大變化。因此，利率的變動通常不被納入考量。如果您正考慮購買長期選擇權LEAPS，而其間利率預期將升高或下降，您就需要考慮到Rho的影響。

利率是選擇權定價模型中的一個重要參數。一般來說，在其他條件不變的情況下，利率上升往往會使買權選擇權的價格上漲，同時使賣權選擇權的價格下降。例如，當前利率為3%，某個$100買權的Rho值為+0.45，假設其他定價因素保持不變，當利率上升至4%，該買權的溢價將上升$0.45。相對地，如果某個賣權的Rho值為-.45，則賣權溢價將下降$0.45。

在利率上升的環境下，買權的價值通常會增加。因為當利率上升，投資者對投資回報率要求也會更高。因為持有股票的機會成本增加，相比直接購買股票，購買買權是更有效利用資本的方法，因為持有買權需要的資本遠少於購買相等數量的股票。節省下來的資金隨後可以投資於收益較高的投資品，如債券。